Por Emilio Oropeza aka Drummer (@drummer7212)
Descripción
El reto nos proporciona el código server.py, el cual se estuvo ejecutando en un servidor.
Al conectarnos al servidor podemos ejecutar comandos básicos de Linux, por ejemplo, ls o dir, como se muestra en la ilustración 2, para ello, se envía un carácter (el que sea) y el comando a ejecutar.
Analizando el comportamiento del código se deduce que los comandos ls y dir, se pueden ejecutar sin ningún problema y con los argumentos que uno guste. Si se trata de ejecutar el comando cat o cd se imprime el mensaje Signature verification check failed, por lo tanto, al indagar más en el código podemos observar que con el comando sign se obtiene la firma RSA del comando o frase enviada, para esto se hace la prueba con los comandos exit y leave, que deben de ser enviados codificados en base64, los cuales resultan exitosos cuando se manda la firma que hemos obtenido junto con el comando, ver ilustración 3.
Al tratar de obtener la firma de los comandos cat o cd, se muestra el mensaje Invalid Command, ver ilustración 4. Por lo que se trata de buscar un ataque para bypassear la condición o buscar un ataque que corresponda.
Al investigar, se encuentra un ataque para RSA que se llama Blind.
Teoría
Firma Digital:
En cifrado asimétrico existen dos llaves llave pública y llave privada, cuando usamos la llave pública para cifrar el mensaje, solamente se puede descifrar con la llave privada y viceversa. Cuando una persona quiere firmar un mensaje, la persona con la llave privada produce el valor hash del mensaje, elevando éste a la potencia 𝑑 módulo 𝑛, y lo adjunta como “firma” al mensaje. La persona que recibe la firma, usa el mismo algoritmo de hash en conjunto con la llave pública, eleva a la potencia 𝑒 módulo 𝑛 la firma, y compara el resultado del hash junto con el del hash actual del mensaje, ver ilustración 5. Este proceso se puede resumir con la ecuación 1.
Firma Blind
En criptografia, una firma ciega (blind), presentada por David Chaum, es una forma de firma digital en la que el contenido de un mensaje se ofusca antes de enviarlo. La firma ciega resultante puede verificarse públicamente contra el mensaje original, no ofuscado, a la manera de una firma digital regular.
Firma Blind RSA
La versión de firma Blind para RSA usa un valor aleatorio 𝑟 (factor Blind), entre 1 y 𝑛, de manera que 𝑟 es primo a 𝑛, por lo tanto, el autor del mensaje obtiene el mensaje ofuscado calculando la ecuación 2:
Firma RSA Blind Attack
RSA está sujeto al ataque Blind RSA, a través del cual se puede engañar al algoritmo para que descifre un mensaje, firmando ciegamente otro mensaje. Dado que el proceso de firmado es equivalente a descifrar con la clave secreta del firmante, un atacante puede proporcionar una versión ofuscada del mensaje cifrado 𝑚 con la llave pública firmante 𝑚′. El mensaje cifrado usualmente sería información secreta que el atacante observó que se enviaba cifrado bajo la clave pública del firmante sobre la cual el atacante desea obtener información. Cuando el atacante quita la versión ofuscada firmada, tendrá el texto claro, esto se puede observar con las ecuaciones 6,7,8 y 9:
Por ejemplo:
Este reto pertenece a la categoría de Crypto, del concurso Volga CTF 2019, celebrado durante el fin de semana del 29 de marzo del 2019.
Descripción
El reto nos proporciona el código server.py, el cual se estuvo ejecutando en un servidor.
Al analizar el código, como se observa en la ilustración 1, se tienen los valores de 𝑛, 𝑒 y una clase llamada RSA. Por lo que identificamos que es un problema relacionado con este sistema criptográfico.
 |
| Ilustración 1 Analizando código |
 |
| Ilustración 2 Prueba de comando ls |
 |
| Ilustración 3 Firma del comando exit |
 |
| Ilustración 4 Resultado del intento de firma del comando cat |
Teoría
Firma Digital:
En cifrado asimétrico existen dos llaves llave pública y llave privada, cuando usamos la llave pública para cifrar el mensaje, solamente se puede descifrar con la llave privada y viceversa. Cuando una persona quiere firmar un mensaje, la persona con la llave privada produce el valor hash del mensaje, elevando éste a la potencia 𝑑 módulo 𝑛, y lo adjunta como “firma” al mensaje. La persona que recibe la firma, usa el mismo algoritmo de hash en conjunto con la llave pública, eleva a la potencia 𝑒 módulo 𝑛 la firma, y compara el resultado del hash junto con el del hash actual del mensaje, ver ilustración 5. Este proceso se puede resumir con la ecuación 1.
ℎ = ℎ𝑎𝑠ℎ(𝑚); (ℎ^𝑒)^𝑑 = ℎ^(𝑒𝑑) = ℎ^(𝑑𝑒) = (ℎ^𝑑)^𝑒 ≡ ℎ (𝑚𝑜𝑑 𝑛) (1)
 |
| Ilustración 5 Firma Digital |
Firma Blind
En criptografia, una firma ciega (blind), presentada por David Chaum, es una forma de firma digital en la que el contenido de un mensaje se ofusca antes de enviarlo. La firma ciega resultante puede verificarse públicamente contra el mensaje original, no ofuscado, a la manera de una firma digital regular.
Firma Blind RSA
La versión de firma Blind para RSA usa un valor aleatorio 𝑟 (factor Blind), entre 1 y 𝑛, de manera que 𝑟 es primo a 𝑛, por lo tanto, el autor del mensaje obtiene el mensaje ofuscado calculando la ecuación 2:
𝑚′ = 𝑚*(𝑟^𝑒) 𝑚𝑜𝑑 𝑛 (2)
donde 𝑚′ es el mensaje ofuscado, este mensaje se envía a la autoridad que lo firmará, se firma el mensaje con la ecuación 3:
𝑠′ = (𝑚′)^𝑑 𝑚𝑜𝑑 𝑛 (3)
donde 𝑠′ es la firma blind, éste se envía al autor del mensaje, que puede remover el factor blind para obtener 𝑠, la firma RSA válida de 𝑚, ecuación 4:
𝑠 = 𝑠′ ∗ 𝑟−1 𝑚𝑜𝑑 𝑛 (4)
Esto se puede demostrar en la ecuación 5:
𝑠′ = (𝑚(𝑟^𝑒))^𝑑 = (𝑚^𝑑)*𝑟(𝑚𝑜𝑑 𝑛) ∴ 𝑠′/𝑟 = (𝑚^𝑑)𝑟/𝑟(𝑚𝑜𝑑 𝑛) = 𝑚^𝑑 (𝑚𝑜𝑑 ) = 𝑠 (5)
Firma RSA Blind Attack
RSA está sujeto al ataque Blind RSA, a través del cual se puede engañar al algoritmo para que descifre un mensaje, firmando ciegamente otro mensaje. Dado que el proceso de firmado es equivalente a descifrar con la clave secreta del firmante, un atacante puede proporcionar una versión ofuscada del mensaje cifrado 𝑚 con la llave pública firmante 𝑚′. El mensaje cifrado usualmente sería información secreta que el atacante observó que se enviaba cifrado bajo la clave pública del firmante sobre la cual el atacante desea obtener información. Cuando el atacante quita la versión ofuscada firmada, tendrá el texto claro, esto se puede observar con las ecuaciones 6,7,8 y 9:
𝑚′′ = 𝑚′(𝑟^𝑒) 𝑚𝑜𝑑 𝑛 (6)
= (𝑚^𝑒 𝑚𝑜𝑑 𝑛 ∗ 𝑟^𝑒) 𝑚𝑜𝑑 𝑛
= (𝑚𝑟)^𝑒 𝑚𝑜𝑑 𝑛 (7)
Donde 𝑚′ es la versión cifrada del mensaje. Cuando el mensaje es firmado, el texto claro 𝑚 se extrae fácilmente.
𝑠′ = (𝑚′′)^𝑑 𝑚𝑜𝑑 𝑛 (8)
= ((𝑚𝑟)^𝑒 𝑚𝑜𝑑 𝑛)^𝑑 𝑚𝑜𝑑 𝑛
= (𝑚𝑟)^(𝑒𝑑) 𝑚𝑜𝑑 𝑛
= 𝑚 ∗ 𝑟 𝑚𝑜𝑑 𝑛,𝑡𝑎𝑙 𝑞𝑢𝑒 𝑒𝑑 ≡ 1 𝑚𝑜𝑑 ∅(𝑛) (9)
Donde ∅(𝑛) refiere a la función de Euler, por lo tanto el mensaje se obtiene fácilmente de la ecuación 10:
𝑚 = 𝑠′ ∗ 𝑟^(−1) 𝑚𝑜𝑑 𝑛 (10)
Por ejemplo:
- Tenemos los valores:
- n=133
- e=5
- d=65
- dónde el mensaje a firmar es 10:
- m=10
- La firma se calcula con la siguiente ecuación:
- 𝑠 = 𝑚^𝑑 𝑚𝑜𝑑 𝑛
- 𝑠 = 1065 𝑚𝑜𝑑 133 = 33
- La firma del mensaje es 33, ahora supongamos que no podemos firmar 10, en el caso del problema cat, pero aún queremos obtener el valor de la firma, escogemos el mensaje ofuscado, en este caso 3:
- r=3
- El valor es elevado a la potencia de 𝑒 y lo multiplica por el mensaje original 𝑚 𝑚𝑜𝑑 𝑛:
- 𝑚1 = 𝑚 ∗ 𝑟^𝑒 𝑚𝑜𝑑 𝑛
- 𝑚1 = 10 ∗ 35 𝑚𝑜𝑑 133 = 36
- Ahora el mensaje modificado 𝑚1 no contiene el valor 10. Por lo que ahora podemos hacer que se firme el mensaje:
- 𝑠1 = 𝑚1^𝑑 𝑚𝑜𝑑
- 𝑠1 = 3665 𝑚𝑜𝑑 133 = 99
- Para restaurar la firma del mensaje 𝑠 de 𝑠1 necesitamos multiplicarle el inverso de r, en este caso el valor es 89, por lo tanto:
- 𝑠 = 𝑠1 ∗ 𝑟𝑖𝑛𝑣𝑒𝑟𝑠𝑜 𝑚𝑜𝑑 𝑛
- 𝑠 = 99 ∗ 89 𝑚𝑜𝑑 133 = 33
- Con esto obtenemos la firma del mensaje original.
Para escoger el valor de r, se debe de cumplir la condición de 𝑚𝑐𝑑(𝑟,𝑛) = 1, donde 𝑟 puede tener muchos valores ya que n es el producto de 2 números primos.
Problema
En nuestro caso, implementamos un script, como se puede ver en la ilustración 6, el cual itera nuestro mensaje 𝑚 sobre distintos valores de 𝑟, verificando que el mensaje modificado y el valor de retorno de una llamada shlex.split() sean los mismos. El valor del reto original es r=6631, ver ilustración 7.
Nota: El valor del reto modificado, que está en la plataforma es r=5.
Implementando las ecuaciones en un script para obtener la bandera, ver ilustración 8, obtenemos primero el mensaje modificado, lo ajustamos y codificamos para que posteriormente se establezca la conexión al servidor, firmamos el mensaje modificado para obtener la firma, posteriormente calculamos la firma del mensaje original y lo enviamos al servidor para obtener la bandera, el código quedó de esta forma:
Al ejecutarlo, como se muestra en la ilustración 9, obtenemos la bandera:
Gracias a f99942 y a Oniriko, por su apoyo en la realización de este blog.
Go Mayas!
Bibliografía
AUMASSON, Jean-Philippe. Serious Cryptography: A Practical Introduction to Modern Encryption. No Starch Press. E.U.A. 2017.
SCHNEIER, Bruce. Applied Cryptography: Protocols, Algorithms and Source Code in C. Wiley. E.U.A. 2015.
Problema
En nuestro caso, implementamos un script, como se puede ver en la ilustración 6, el cual itera nuestro mensaje 𝑚 sobre distintos valores de 𝑟, verificando que el mensaje modificado y el valor de retorno de una llamada shlex.split() sean los mismos. El valor del reto original es r=6631, ver ilustración 7.
 |
| Ilustración 6 Código para obtener factor blind |
 |
| Ilustración 7 Valor del factor blind |
Implementando las ecuaciones en un script para obtener la bandera, ver ilustración 8, obtenemos primero el mensaje modificado, lo ajustamos y codificamos para que posteriormente se establezca la conexión al servidor, firmamos el mensaje modificado para obtener la firma, posteriormente calculamos la firma del mensaje original y lo enviamos al servidor para obtener la bandera, el código quedó de esta forma:
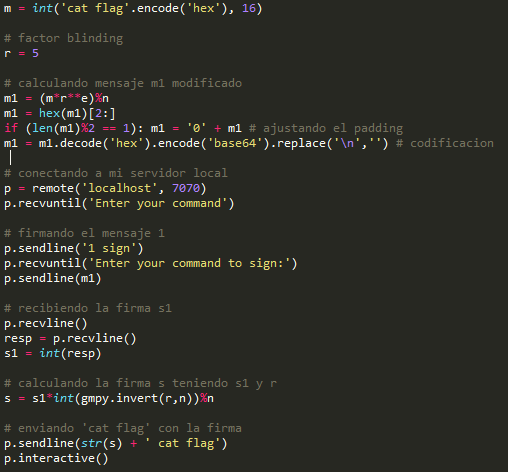 |
| Ilustración 8 Solución al reto |
 |
| Ilustración 9 Bandera |
Go Mayas!
Bibliografía
AUMASSON, Jean-Philippe. Serious Cryptography: A Practical Introduction to Modern Encryption. No Starch Press. E.U.A. 2017.
SCHNEIER, Bruce. Applied Cryptography: Protocols, Algorithms and Source Code in C. Wiley. E.U.A. 2015.
Excelente aporte bro
ResponderBorrar